|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
On Oscillation of
Second-Order Delay Dynamic Equations on Time Scales
Author(s):
S. H. Saker
Department of Mathematics, Faculty of Science,
Mansoura University, Mansoura, 35516,
Egypt.
shsaker@mans.edu.eg
Abstract:
Some new oscillation criteria for second-order linear delay dynamic equation
on a time scale T are established. Our results improve the
recent results for delay dynamic equations and in the special case when
T=R, the results include the oscillation results established by Hille [1948,
Trans. Amer. Math. Soc. 64 (1948), 234-252] and Erbe [Canad. Math. Bull. 16
(1973), 49-56.] for differential equations. When T=Z the
results include and improve some oscillation criteria for difference
equations. When T=hZ, h>0, T=qN and T=N2, i.e., for generalized second order delay difference equations our
results are essentially new and can be applied on different types of time
scales. An example is considered to illustrate the main results.
Paper's Title:
On the Biharmonic Equation with Nonlinear Boundary Integral Conditions
Author(s):
R. Hamdouche and H. Saker
L.M.A. Department of Mathematics, Faculty
of Sciences,
University of Badji Mokhtar,
P.O.Box 12. Annaba 23000,
Algeria.
E-mail: h_saker@yahoo.fr,
hmdch.rahma16@gmail.com
Abstract:
In the present work, we deal with the biharmonic problems in a bounded domain in the plane with the nonlinear boundary integral conditions. After applying the Boundary integral method, a system of nonlinear boundary integral equations is obtained. The result show that when the nonlinearity satisfies some conditions lead the existence and uniqueness of the solution.
Paper's Title:
Oscillatory Behavior of Second-Order Non-Canonical
Retarded Difference Equations
Author(s):
G.E. Chatzarakis1, N. Indrajith2, E. Thandapani3 and K.S. Vidhyaa4
1Department
of Electrical and Electronic Engineering Educators,
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
geaxatz@otenet.gr
2Department
of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com
3Ramanujan
Institute for Advanced Study in Mathematics,
University of Madras,
Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in
4
Department of Mathematics,Abstract:
Using monotonic properties of nonoscillatory solutions, we obtain new oscillatory criteria for the second-order non-canonical difference equation with retarded argument
![]()
Our oscillation results improve and extend the earlier ones. Examples illustrating the results are provided.
Paper's Title:
Oscillation Criteria for Second Order Delay Difference Equations via Canonical Transformations and Some New Monotonic Properties
Author(s):
R. Deepalakhmi, S. Saravanan, J. R. Graef, and E. Thandapani
Department of Interdisciplinary Studies
Tamil Nadu Dr. Ambedkar Law University
Chennai-600113,
India.
profdeepalakshmi@gmail.com
Madras School of Economics,
Chennai-600025,
India.
profsaran11@gmail.com
Department of Mathematics,
University of Tennessee at Chattanooga,
Chattanooga,TN 37403,
USA.
john-graef@utc.edu
Ramanujan Institute for Advanced Study in
Mathematics,
University of Madras,
Chennai - 600 005,
India.
ethandapani@yahoo.co.in
Abstract:
This paper is concerned with second-order linear noncanonical delay difference equations of the form
Δ(μ(t)Δ y(t))+ p(t)y(φ(t))=0.
The authors prove new oscillation criteria by first transforming the equation into canonical form and then obtaining some new monotonic properties of the positive solutions of the transformed equation. By using a comparison with first-order delay difference equations and a generalization of a technique developed by Koplatadze, they obtain their main results. Examples illustrating the improvement over known results in the literature are presented.
Paper's Title:
Improved Oscillation Criteria of Second-Order Advanced Non-canonical Difference Equation
Author(s):
G. E. Chatzarakis1, N. Indrajith2, S. L. Panetsos1, E. Thandapani3
1Department
of Electrical and Electronic Engineering Educators
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
geaxatz@otenet.gr
spanetsos@aspete.gr
2Department
of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com
3Ramanujan
Institute for Advanced Study in Mathematics,
University of Madras Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in
Abstract:
Employing monotonic properties of nonoscillatory solutions, we derive some new oscillation criteria for the second-order advanced non-canonical difference equation
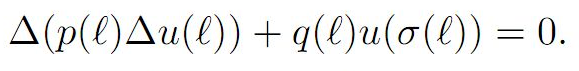
Our results extend and improve the earlier ones. The outcome is illustrated via some particular difference equations.
Search and serve lasted 1 second(s).