Paper's Title:

Some New Inequalities of Hermite-Hadamard and Fejér Type for Certain Functions with Higher Convexity

Author(s):

Steven G. From

Department of Mathematics,
University of Nebraska at Omaha,
Omaha, Nebraska 68182-0243,
U.S.A.
E-mail: sfrom@unomaha.edu

Abstract:

In this paper, we present some new inequalities of Hermite-Hadamard or Fejér type for certain functions satisfying some higher convexity conditions on one or more derivatives.
An open problem is given also.
Some applications to the logarithmic mean are given.

Paper's Title:

Further Bounds for Two Mappings Related to the Hermite-Hadamard Inequality

Author(s):

S. S. Dragomir^1,2 and I. Gomm¹

¹Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428, Melbourne City, MC 8001,
Australia.

²School of Computational & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.

sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir  
 

Abstract:

Some new results concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for twice differentiable functions with applications for special means are given.

Paper's Title:

Bounds for Two Mappings Associated to the Hermite-Hadamard Inequality

Author(s):

S. S. Dragomir^1,2 and I. Gomm¹

¹Mathematics, School of Engineering & Science,
Victoria University,
PO Box 14428, Melbourne City, MC 8001,
Australia.

²School of Computational & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.

sever.dragomir@vu.edu.au
ian.gomm@vu.edu.au
URL: http://rgmia.org/dragomir  
 

Abstract:

Some inequalities concerning two mappings associated to the celebrated Hermite-Hadamard integral inequality for convex function with applications for special means are given.

Paper's Title:

Some Applications of Fejér's Inequality for Convex Functions (I)

Author(s):

S.S. Dragomir^1,2 and I. Gomm¹

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia.

sever.dragomir@vu.edu.au

URL: http://rgmia.org/dragomir

²School of Computational & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.

Abstract:

Some applications of Fejér's inequality for convex functions are explored. Upper and lower bounds for the weighted integral

under various assumptions for f with applications to the trapezoidal quadrature rule are given. Some inequalities for special means are also provided

Paper's Title:

Inequalities for the Area Balance of Functions of Bounded Variation

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

We introduce the area balance function associated to a Lebesgue integrable function f:[a,b] →C by

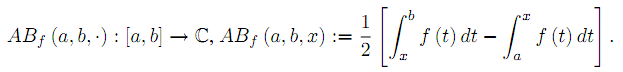
Several sharp bounds for functions of bounded variation are provided. Applications for Lipschitzian and convex functions are also given.

Paper's Title:

Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.

Search and serve lasted 1 second(s).