|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Multivalent Harmonic Mappings Convoluted With a Multivalent Analytic Function
Author(s):
Om P. Ahuja and Özlem Güney
Kent State University, Department of Mathematical Sciences,
14111, Claridon-Troy Road, Burton, Ohio 44021,
U.S.A.
oahuja@kent.edu
University of Dicle, Department of Mathematics, Abstract:
The object of this paper is to study certain geometric properties of
a family of multivalent harmonic mappings in the plane convoluted
with a multivalent analytic function in the open unit disc. Paper's Title:
Fekete-Szegö Inequality for Sakaguchi Type of functions in Petal Shaped Domain Author(s):
E. K. Nithiyanandham and B. Srutha Keerthi Division of Mathematics, School of
Advanced Sciences, Division of Mathematics, School of
Advanced Sciences, Abstract:
In this paper, we estimate coefficient bounds,|a_2|,|a_3| and |a_4|, Fekete-Szegö inequality
the function being holomorphic, we expand using Taylor series and obtain several corollaries and consequences for the main result. Paper's Title:
Toeplitz Determinant for Sakaguchi Type Functions Under Petal Shaped Domain Author(s):
B. Nandhini and B. Srutha Keerthi Division of Mathematics, School of
Advanced Sciences, Division of Mathematics, School of
Advanced Sciences, Abstract:
We introduce a new general subclass GPt,ρ of Sakaguchi kind function on a Petal shaped domain. We obtain
coefficients bounds and upper bounds for the Fekete-Szegö
functional over the class. From these functions we obtain the bounds of first four coefficients, and then we have derived the Toeplitz determinant
T2(2) and T3(1) whose diagonal entries are the coefficients of functions. Paper's Title:
On Certain Classes of Harmonic Univalent Functions Based on Salagean Operator Author(s):
G. Murugusundaramoorthy, Thomas Rosy, and B. A. Stephen Department of Applied Mathematics and Informatics,
Department of Applied Mathematics and Informatics,
Abstract:
We define and investigate a class of complex-valued harmonic univalent functions of the form f = h + g using Salagean operator where h and g are analytic in the unit disc U = { z : |z| < 1 }. A necessary and sufficient coefficient conditions are given for functions in these classes. Furthermore, distortion theorems, inclusion relations, extreme points, convolution conditions and convex combinations for this family of harmonic functions are obtained.
Paper's Title:
Fekete-Szegö Problem for Univalent Functions with Respect to k-Symmetric
Points Author(s):
K. Al-Shaqsi and M. Darus
School of Mathematical Sciences, Faculty of Science and Technology, Abstract:
In the present investigation, sharp upper bounds of |a3- μa22|
for functions f(z) = z + a2z2 + a2z3 + ... belonging to certain subclasses
of starlike and convex functions with respect to k-symmetric points are
obtained. Also certain applications of the main results for subclasses of
functions defined by convolution with a normalized analytic function are
given. In particular, Fekete- Szeg
Faculty of Science and Art, 21280 Diyarbakir,
Turkey
ozlemg@dicle.edu.tr
2: Paper Source
PDF document
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: nithiyankrish@gmail.com
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com ![]() and Toeplitz determinant
T2(2) and T3(1) for functions belonging to the following class
and Toeplitz determinant
T2(2) and T3(1) for functions belonging to the following class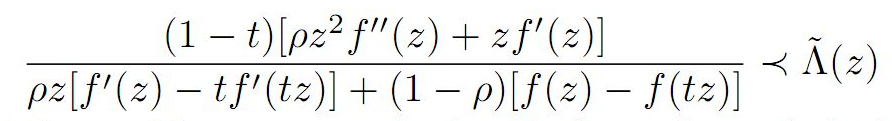
2: Paper Source
PDF document
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail:
nandhinibaskar1996@gmail.com
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com
1: Paper Source
PDF document
Department of Mathematics, Vellore Institute of Technology,
Deemed University, Vellore - 632014, India.
gmsmoorthy@yahoo.com
Department of Mathematics, Madras Christian College,
Chennai - 600059, India.
drthomasrosy@rediffmail.com
1: Paper Source
PDF document
University Kebangsaan Malaysia,
Bangi 43600 Selangor D. Ehsan,
Malaysia
ommath@hotmail.com
maslina@ukm.my
Search and serve lasted 0 second(s).