Paper's Title:

Existence of Non-spurious Solutions to Discrete Boundary Value Problems

Author(s):

Irena Rachunkova and Christopher C. Tisdell

Department of Mathematics
Palacky University
771 46 Olomouc, Czech Republic.
rachunko@risc.upol.cz
URL: http://phoenix.inf.upol.cz/~rachunekl/mathair/matha-en.htm

School of Mathematics
The University of New South Wales
Sydney 2052, Australia.
cct@unsw.edu.au
URL: http://www.maths.unsw.edu.au/~cct

Abstract:

This paper investigates discrete boundary value problems (BVPs) involving second-order difference equations and two-point boundary conditions. General theorems guaranteeing the existence and uniqueness of solutions to the discrete BVP are established. The methods involve a sufficient growth condition to yield an a priori bound on solutions to a certain family of discrete BVPs. The em a priori bounds on solutions to the discrete BVP do not depend on the step-size and thus there are no ``spurious'' solutions. It is shown that solutions of the discrete BVP will converge to solutions of ordinary differential equations.

Paper's Title:

Positive Periodic Time-Scale Solutions for Functional Dynamic Equations

Author(s):

Douglas R. Anderson and Joan Hoffacker

Department of Mathematics and Computer Science
Concordia College
Moorhead, MN 56562 USA
andersod@cord.edu
URL: http://www.cord.edu/faculty/andersod/

Department of Mathematical Sciences
Clemson University
Clemson, SC 29634 USA
johoff@clemson.edu
URL: http://www.math.clemson.edu/facstaff/johoff.htm

Abstract:

Using Krasnoselskii's fixed point theorem, we establish the existence of positive periodic solutions to two pairs of related nonautonomous functional delta dynamic equations on periodic time scales, and then extend the discussion to higher-dimensional equations. Two pairs of corresponding nabla equations are also provided in an analogous manner.

Paper's Title:

On Oscillation of Second-Order Delay Dynamic Equations on Time Scales

Author(s):

S. H. Saker

Department of Mathematics, Faculty of Science,
Mansoura University, Mansoura, 35516,
Egypt.
shsaker@mans.edu.eg

Abstract:

Some new oscillation criteria for second-order linear delay dynamic equation on a time scale T are established. Our results improve the recent results for delay dynamic equations and in the special case when T=R, the results include the oscillation results established by Hille [1948, Trans. Amer. Math. Soc. 64 (1948), 234-252] and Erbe [Canad. Math. Bull. 16 (1973), 49-56.] for differential equations. When T=Z the results include and improve some oscillation criteria for difference equations. When T=hZ, h>0, T=q^N and T=N², i.e., for generalized second order delay difference equations our results are essentially new and can be applied on different types of time scales. An example is considered to illustrate the main results.

Paper's Title:

Comparison Results for Solutions of Time Scale Matrix Riccati Equations and Inequalities

Author(s):

R. Hilscher

Department of Mathematical Analysis, Faculty of Science,
Masaryk University, Janáčkovo nám. 2a,
CZ-60200, Brno, Czech Republic.
hilscher@math.muni.cz
URL: http://www.math.muni.cz/~hilscher/

Abstract:

In this paper we derive comparison results for Hermitian solutions of time scale matrix Riccati equations and Riccati inequalities. Such solutions arise from special conjoined bases (X,U) of the corresponding time scale symplectic system via the Riccati quotient 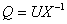. We also discuss properties of a unitary matrix solution 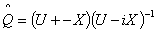of a certain associated Riccati equation.

Paper's Title:

Oscillation and Boundedness of Solutions to First and Second Order Forced Dynamic Equations with Mixed Nonlinearities

Author(s):

Ravi P. Agarwal and Martin Bohner

Department of Mathematical Sciences, Florida Institute of Technology
Melbourne, FL 32901,
U.S.A.
bohner@mst.edu
URL:http://web.mst.edu/~bohner

Department of Economics and Finance, Missouri University of Science and Technology
Rolla, MO 65401,
U.S.A.
agarwal@fit.edu

Abstract:

Some oscillation and boundedness criteria for solutions to certain first and second order forced dynamic equations with mixed nonlinearities are established. The main tool in the proofs is an inequality due to Hardy, Littlewood and Pólya. The obtained results can be applied to differential equations, difference equations and q-difference equations. The results are illustrated with numerous examples.

Search and serve lasted 1 second(s).