|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
A Different Proof for the non-Existence of Hilbert-Schmidt Hankel Operators with
Anti-Holomorphic Symbols on the Bergman Space
Author(s):
Georg Schneider
Universität Wien, Brünnerstr. 72 A-1210 Wien,
Austria.
georg.schneider@univie.ac.at
URL: http://www.univie.ac.at/bwl/cont/mitarbeiter/schneider.htm
Abstract:
We show that there are no (non-trivial) Hilbert-Schmidt Hankel
operators with anti-holomorphic symbols on the Bergman space of
the unit-ball B2(Bl) for l≥2. The result dates back to
[6]. However, we give a different proof. The methodology can
be easily applied to other more general settings. Especially, as
indicated in the section containing generalizations, the new
methodology allows to prove some robustness results for existing
ones.
Paper's Title:
Isoperimetric Inequalities for Dual Harmonic Quermassintegrals
Author(s):
Yuan Jun, Zao Lingzhi and Duan Xibo
School of Mathematics and Computer Science,
Nanjing Normal University, Nanjing, 210097,
China.
yuanjun_math@126.com
Department of Mathematics, Nanjing Xiaozhuang University,
Nanjing, 211171,
China.
lzhzhao@163.com
Department of Mathematics, Shandong Water Polytechnic,
Shandong, 276826,
China
dxb1111@sohu.com
Abstract:
In this paper, some isoperimetric inequalities for the dual harmonic
quermassintegrals are established.
Paper's Title:
An Easy and Efficient Way for Solving A class of Singular Two Point Boundary Value Problems
Author(s):
Muhammed I. Syam, Muhammed N. Anwar and Basem S. Attili
Mathematical Sciences Department
United Arab Emirates University, P. O. Box 17551
Al-Ain, United Arab Emirates
b.attili@uaeu.ac.ae
Abstract:
We will consider an efficient and easy way for solving a certain
class of singular two point boundary value problems. We will
employ the least squares method which proved to be efficient for
this type of problems. Enough examples that were considered by
others will be solved with comparison with the results presented
there.
Paper's Title:
Note on the Rank of Birkhoff Interpolation
Author(s):
J. Rubió-Massegú
Applied Mathematics III, Universitat Politècnica de Catalunya,
Colom 1, 08222, Terrassa,
Spain
josep.rubio@upc.edu
Abstract:
The relationship between a variant of the rank of a univariate
Birkhoff interpolation problem, called normal rank, and other
numbers of interest associated to the interpolation problem is
studied.
Paper's Title:
Wavelet Frames in Higher Dimensional Sobolev Spaces
Author(s):
Raj Kumar, Manish Chauhan, and Reena
Department of Mathematics,
Kirori Mal College, University of Delhi,
New Delhi-110007,
India.
E-mail: rajkmc@gmail.com
Department of Mathematics,
University of Delhi,
New Delhi-110007,
India
E-mail: manish17102021@gmail.com
Department of Mathematics,
Hans Raj College, University of Delhi,
New Delhi-110007,
India
E-mail: reena.bhagwat29@gmail.com
Abstract:
In this paper, we present sufficient condition for the sequence
of vectors
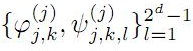to be a frame for Hs(Rd) are derived. Necessary and
sufficient conditions for the sequence of vectors
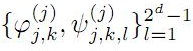to be tight wavelet frames in Hs(Rd) are obtained.
Further, as an application an example of tight wavelet frames for Hs(R2) as bivariate box spline over 3-direction are given.
Search and serve lasted 0 second(s).