|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Common Fixed Point Results for Banach Operator Pairs and Applications to Best Approximation
Author(s):
Hemant Kumar Nashine
Department of Mathematics,
Disha Institute of Management and Technology,
Satya Vihar, Vidhansabha - Chandrakhuri Marg (Baloda Bazar Road),
Mandir Hasaud,
Raipur - 492101(Chhattisgarh), India.
hemantnashine@rediffmail.com
nashine_09@rediffmail.com
Abstract:
The common fixed point results for Banach operator pair with generalized nonexpansive mappings in q-normed space have been obtained in the present work. As application, some more general best approximation results have also been determined without the assumption of linearity or affinity of mappings. These results unify and generalize various existing known results with the aid of more general class of noncommuting mappings.
Paper's Title:
On the Class of Totally Polynomially Posinormal Operators
Author(s):
E. Shine Lal, T. Prasad, P. Ramya
Department of Mathematics,University
College,
Thiruvananthapuram, Kerala, 695034.
India.
E-mail: shinelal.e@gmail.com
Department of Mathematics,
University of Calicut,
Malapuram, Kerala 673635,
India.
E-mail: prasadvalapil@gmail.com
Department of Mathematics,
N.S.S College,
Nemmara, Kerala, 678508
India.
E-mail: ramyagcc@gmail.com
Abstract:
In this paper, we proved that if T ∈
B(H) is totally P-posinormal operator with
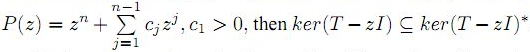. Moreover, we study spectral continuity and range kernel orthogonality of these class of operators.
Paper's Title:
Algorithms for Nonlinear Problems Involving Strictly Pseudocontractive Mappings
Author(s):
Mathew Olajiire Aibinu1, Surendra Colin Thakur2, Sibusiso Moyo3
1Institute for Systems Science
& KZN E-Skill CoLab,
Durban University of Technology,
Durban 4000,
South Africa.
1DSI-NRF
Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS),
Johannesburg,
South Africa.
E-mail: moaibinu@yahoo.com
mathewa@dut.ac.za
2 KZN E-Skill CoLab,
Durban University of Technology,
Durban 4000,
South Africa.
E-mail: thakur@dut.ac.za
3Institute for Systems Science & Office of the DVC Research,
Innovation & Engagement Milena Court,
Durban University of Technology,
Durban 4000,
South Africa.
E-mail: dvcrie@dut.ac.za
Abstract:
The puzzles in approximating a fixed point of nonlinear problems involving the class of strictly pseudocontractive mappings are conquered in this paper through viscosity implicit rules. Using generalized contraction mappings, a new viscosity iterative algorithm which is implicit in nature is proposed and analysed in Banach spaces for the class of strictly pseudocontractive mappings. The computations and analysis which are used in the proposed scheme are easy to follow and this gives rooms for a broad application of the scheme. It is obtained that the proposed iterative algorithm converges strongly to a fixed point of a μ-strictly pseudocontractive mapping which also solves a variational inequality problem. The result is also shown to hold for finite family of strictly pseudocontractive mappings. A numerical example is given to show the skillfulness of the proposed scheme and its implementation.
Paper's Title:
A new approach to the study of fixed point for simulation functions with application in G-metric spaces
Author(s):
Komi Afassinou and Ojen Kumar Narain
Department of Mathematical Sciences,
University of Zululand,
KwaDlangezwa,
South Africa.
E-mail: komia@aims.ac.za
School of Mathematics, Statistics and
Computer Science,
University of KwaZulu-Natal, Durban,
South Africa.
E-mail: naraino@ukzn.ac.za
Abstract:
The purpose of this work is to generalize the fixed point results of Kumar et al. [11] by introducing the concept of (α,β)-Z-contraction mapping, Suzuki generalized (α,β)-Z-contraction mapping, (α,β)-admissible mapping and triangular (α,β)-admissible mapping in the frame work of G-metric spaces. Fixed point theorems for these class of mappings are established in the frame work of a complete G-metric spaces and we establish a generalization of the fixed point result of Kumar et al. [11] and a host of others in the literature. Finally, we apply our fixed point result to solve an integral equation.
Search and serve lasted 0 second(s).