|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Application of Equivalence Method to Classify Monge-Ampère Equations of Elliptic Type
Author(s):
Moheddine Imsatfia
E-mail: imsatfia@math.jussieu.fr
Abstract:
In this paper, we apply Cartan's equivalence method to give a local classification of Monge-Ampère equations of elliptic type. Then we find a necessary and sufficient conditions such that a Monge-Ampère equation is either contactomorphic to the Laplace equation or to an Euler-Lagrange equation.
Paper's Title:
Ostrowski Type Fractional Integral Inequalities for Generalized (s,m,
Author(s):
Artion Kashuri and Rozana Liko
University of Vlora "Ismail Qemali",
Faculty of Technical Science,
Department of Mathematics, 9400,
Albania.
E-mail:
artionkashuri@gmail.com
E-mail: rozanaliko86@gmail.com
Abstract:
In the present paper, the notion of generalized (s,m,φ)-preinvex function is introduced and some new integral inequalities for the left hand side of Gauss-Jacobi type quadrature formula involving generalized (s,m,φ)-preinvex functions along with beta function are given. Moreover, some generalizations of Ostrowski type inequalities for generalized (s,m,φ)-preinvex functions via Riemann-Liouville fractional integrals are established.
Paper's Title:
Ostrowski Type Inequalities for Lebesgue Integral: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics, School of Engineering
& Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
http://rgmia.org/dragomir
Abstract:
The main aim of this survey is to present recent results concerning Ostrowski type inequalities for the Lebesgue integral of various classes of complex and real-valued functions. The survey is intended for use by both researchers in various fields of Classical and Modern Analysis and Mathematical Inequalities and their Applications, domains which have grown exponentially in the last decade, as well as by postgraduate students and scientists applying inequalities in their specific areas.
Paper's Title:
Improved Oscillation Criteria of Second-Order Advanced Non-canonical Difference Equation
Author(s):
G. E. Chatzarakis1, N. Indrajith2, S. L. Panetsos1, E. Thandapani3
1Department
of Electrical and Electronic Engineering Educators
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
geaxatz@otenet.gr
spanetsos@aspete.gr
2Department
of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com
3Ramanujan
Institute for Advanced Study in Mathematics,
University of Madras Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in
Abstract:
Employing monotonic properties of nonoscillatory solutions, we derive some new oscillation criteria for the second-order advanced non-canonical difference equation
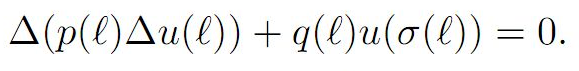
Our results extend and improve the earlier ones. The outcome is illustrated via some particular difference equations.
Search and serve lasted 0 second(s).