|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
C*-valued metric projection and Moore-Penrose inverse on Hilbert C*-modules
Author(s):
M. Eshaghi Gordji, H. Fathi and S.A.R. Hosseinioun
Department of Mathematics,
Semnan University, P.O. Box 35195-363, Semnan,
Iran.
Center of Excellence in Nonlinear Analysis and Applications (CENAA),
Semnan University,
Iran.
E-mail: Madjid.Eshaghi@gmail.com
Department of Mathematics,
Shahid Beheshti University, Tehran,
Iran.
E-mail: Hedayat.fathi@yahoo.com
Department of Mathematical Sciences,
University of Arkansas, Fayetteville, Arkansas 72701,
USA.
E-mail: shossein@uark.net
Abstract:
Let t be a regular operator between Hilbert C*-modules and t† be its Moore-Penrose inverse. We give some characterizations for t† based on C*-valued metric projection. Moore-Penrose inverse of bounded operators and elements of a C*-algebra is studied as a special case.
Paper's Title:
Generalized k-distance-balanced Graphs
Author(s):
Amir Hosseini and Mehdi Alaeiyan
Department of mathematics, Karaj Branch,
Islamic Azad university, Karaj,
Iran.
E-mail: amir.hosseini@kiau.ac.ir,
hosseini.sam.52@gmail.com
Department of Mathematics,
Iran University of Science and Technology, Tehran,
Iran.
E-mail: alaeiyan@iust.ac.ir
Abstract:
A nonempty graph Γ is called generalized k-distance-balanced, whenever every edge ab has the following property: the number of vertices closer to a than to b, k, times of vertices closer to b than to a, or conversely, k∈ N .In this paper we determine some families of graphs that have this property, as well as to prove some other result regarding these graphs.
Paper's Title:
Multistage Analytical Approximate Solution of Quasi-Linear Differential- Algebraic System of Index Two
Author(s):
Ibrahim M. Albak, F. A. Abdullah* and Zarita Zainuddin
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 USM, Penang,
Malaysia.
E-mail: ibra13975@gmail.com,
farahaini@usm.my,
zarita@usm.my
Abstract:
In this paper, a new Multistage Transform Method (MSDTM) has been proposed by utilizing a well-known transformation technique, the Differential Transform Method (DTM), to solve Differential Algebraic Equations (DAEs) with index 2. The advantage of the proposed scheme is that it does not require an index reduction and extends the convergence domain of the solution. Some examples for various types of problems are carried out to show the ability of MSDTM in solving DAEs. The results obtained are in good agreement with the existing literature which demonstrates the effectiveness and efficiency of the proposed method.
Paper's Title:
Corrigendum for Multistage Analytical Approximate Solution of Quasi-Linear Differential- Algebraic System of Index Two
Author(s):
Ibrahim M. Albak, F. A. Abdullah* and Zarita Zainuddin
School of Mathematical Sciences,
Universiti Sains Malaysia,
11800 USM, Penang,
Malaysia.
E-mail: ibra13975@gmail.com,
farahaini@usm.my,
zarita@usm.my
Abstract:
This article is a corrigendum to AJMAA Volume 18, Issue 2, Article 13, {PDF Link}.
Paper's Title:
Indonesia's GDP Forecast: Evidence From Fuzzy Time Series Model Using Particle Swarm Optimization Algorithm
Author(s):
Ismail Djakaria1, Djihad Wungguli2, Regina Sugi Pakadang3, Sri Endang Saleh4, Maman Abdurachman Djauhari5
1,2,3Universitas
Negeri Gorontalo,
Department of Statistics, Gorontalo,
Indonesia.
4Universitas Negeri Gorontalo,
Department of Development Economics, Gorontalo,
Indonesia.
5Indonesian Institute of Education,
Jl. Terusan Pahlawan 32, Garut 44151,
Indonesia.
E-mail: iskar@ung.ac.id
URL:
https://orcid.org/0000-0003-1358-2356
Abstract:
Gross Domestic Product (GDP) is a principal indicator used to measure the economic condition of a country. Indonesia's GDP growth from 2017 to 2019 was approximately 6 percent; however, it experienced a decline in 2020 and 2021, with rates of only -0.02 percent and 2.41 percent, respectively. In the process of economic development planning, a forecasting system is required to determine GDP in the future. The forecasting method employed in this research is fuzzy time series optimized using Particle Swarm Optimization (PSO), to enhance the accuracy and convergence of forecasted values. The dataset used comprises secondary data, specifically 54 sets of Indonesian GDP data spanning from the first quarter of 2010 to the second quarter of 2023. The analysis results indicate that the proposed method is better than the conventional fuzzy time series approach. The former method provides a predictive value for one period in the future with a Mean Absolute Percentage Error (MAPE) value of 4.40%. In contrast, the latter yields higher predictive values with a MAPE value of 7.93%.
Paper's Title:
Some New Inequalities for Hypo-q-Norms on a Cartesian Product of Normed Linear Spaces
Author(s):
Sever S. Dragomir1,2
1Applied
Mathematics Research Group, ISILC,
Victoria University,
PO Box 14428, Melbourne City, MC 8001,
Australia.
E-mail: sever.dragomir@vu.edu.au
URL:
http://rgmia.org/dragomir
2School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
Abstract:
Let ( E,|| · ||) be a normed
linear space over the real or complex number field K. If by
Sn,p with p∈[ 1,∞]
we denote the spheres generated by the $p$-norms ||
· ||n,p on Kn, then we consider
the following hypo-q-norms on
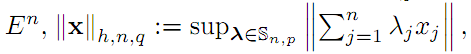with q>1 and
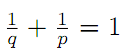if p>1, q=1 if
p=∞
and q=∞ if p=1. For p=2, we also consider the hypo-Euclidean norm on En, i.e.,
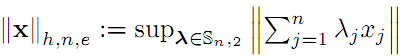
In this paper we have obtained among others the following inequalities
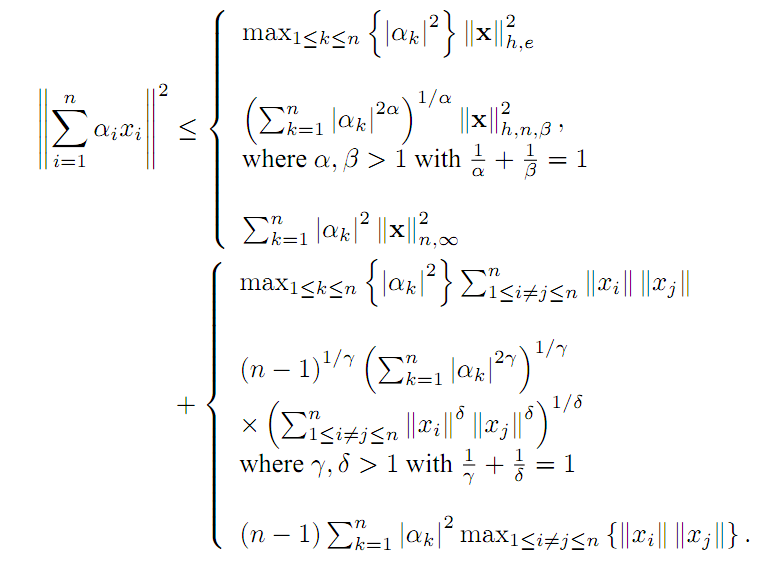
The case for n=2 and the connection with the following new norms
and
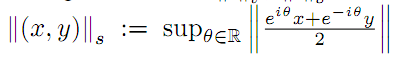
are also investigated. When the norm || · || is generated by an inner product, further bounds are given as well.
Search and serve lasted 1 second(s).