|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Improved Oscillation Criteria of Second-Order Advanced Non-canonical Difference Equation
Author(s):
G. E. Chatzarakis1, N. Indrajith2, S. L. Panetsos1, E. Thandapani3
1Department
of Electrical and Electronic Engineering Educators
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
geaxatz@otenet.gr
spanetsos@aspete.gr
2Department
of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com
3Ramanujan
Institute for Advanced Study in Mathematics,
University of Madras Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in
Abstract:
Employing monotonic properties of nonoscillatory solutions, we derive some new oscillation criteria for the second-order advanced non-canonical difference equation
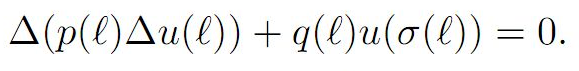
Our results extend and improve the earlier ones. The outcome is illustrated via some particular difference equations.
Paper's Title:
Oscillation Criteria for Second Order Delay Difference Equations via Canonical Transformations and Some New Monotonic Properties
Author(s):
R. Deepalakhmi, S. Saravanan, J. R. Graef, and E. Thandapani
Department of Interdisciplinary Studies
Tamil Nadu Dr. Ambedkar Law University
Chennai-600113,
India.
profdeepalakshmi@gmail.com
Madras School of Economics,
Chennai-600025,
India.
profsaran11@gmail.com
Department of Mathematics,
University of Tennessee at Chattanooga,
Chattanooga,TN 37403,
USA.
john-graef@utc.edu
Ramanujan Institute for Advanced Study in
Mathematics,
University of Madras,
Chennai - 600 005,
India.
ethandapani@yahoo.co.in
Abstract:
This paper is concerned with second-order linear noncanonical delay difference equations of the form
Δ(μ(t)Δ y(t))+ p(t)y(φ(t))=0.
The authors prove new oscillation criteria by first transforming the equation into canonical form and then obtaining some new monotonic properties of the positive solutions of the transformed equation. By using a comparison with first-order delay difference equations and a generalization of a technique developed by Koplatadze, they obtain their main results. Examples illustrating the improvement over known results in the literature are presented.
Paper's Title:
Local and Global Existence and Uniqueness Results for Second and Higher Order Impulsive Functional Differential Equations with Infinite Delay
Author(s):
Johnny Henderson and Abdelghani Ouahab
Department of Mathematics, Baylor University,
Waco, Texas 76798-7328
USA.
Johnny_Henderson@baylor.edu
Laboratoire de Mathématiques, Université de Sidi Bel Abbés
BP 89, 22000 Sidi Bel Abbées,
Algérie.
ouahab@univ-sba.dz
Abstract:
In this paper, we discuss the local and global existence and
uniqueness results for second and higher order impulsive functional
differential equations with infinite delay. We shall rely on a
nonlinear alternative of Leray-Schauder. For the global existence
and uniqueness we apply a recent Frigon and Granas nonlinear
alternative of Leray-Schauder type in Fréchet spaces.
Paper's Title:
Positive Solutions for Systems of Three-point Nonlinear Boundary Value Problems
Author(s):
J. Henderson and S. K. Ntouyas
Department of Mathematics, Baylor University
Waco, Texas
76798-7328 USA.
Johnny_Henderson@baylor.edu
URL: http://www3.baylor.edu/~Johnny_Henderson
Department of Mathematics, University of Ioannina
451 10 Ioannina,
Greece.
sntouyas@cc.uoi.gr
URL: http://www.math.uoi.gr/~sntouyas
Abstract:
Values of λ are determined for which there exist
positive solutions of the system of three-point boundary value problems,
u''(t)+ λa(t)f(v(t))=0, v''(t)+λb(t)g(u(t))=0,
for 0 < t <1, and
satisfying, u(0) = 0, u(1)=α u(η),
v(0) = 0, v(1)=α v(η). A Guo-Krasnosel'skii fixed
point theorem is applied. Paper's Title:
Positive Solutions to a System of Boundary Value Problems for Higher-Dimensional Dynamic Equations on Time Scales Author(s):
I. Y. Karaca Department of Mathematics, URL:
http://ege.edu.tr Abstract:
In this paper, we consider the system of boundary value problems for
higher-dimensional dynamic equations on time scales. We establish
criteria for the existence of at least one or two positive
solutions. We shall also obtain criteria which lead to nonexistence
of positive solutions. Examples applying our results are also given.
Paper's Title:
Oscillatory Behavior of Second-Order Non-Canonical
Retarded Difference Equations Author(s):
G.E. Chatzarakis1, N. Indrajith2, E. Thandapani3 and
K.S. Vidhyaa4 1Department
of Electrical and Electronic Engineering Educators,
2: Paper Source
PDF document
Ege University,
35100 Bornova, Izmir,
Turkey
2: Paper Source
PDF document
School of Pedagogical and Technological Education,
Marousi 15122, Athens,
Greece.
E-mail: gea.xatz@aspete.gr,
geaxatz@otenet.gr
2Department
of Mathematics,
Presidency College, Chennai - 600 005,
India.
E-mail: indrajithna@gmail.com
3Ramanujan
Institute for Advanced Study in Mathematics,
University of Madras,
Chennai - 600 005,
India.
E-mail: ethandapani@yahoo.co.in
4
Department of Mathematics,Abstract:
Using monotonic properties of nonoscillatory solutions, we obtain new oscillatory criteria for the second-order non-canonical difference equation with retarded argument
![]()
Our oscillation results improve and extend the earlier ones. Examples illustrating the results are provided.
Search and serve lasted 0 second(s).