|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Fixed Point Results for Integral Type Contractions in R-Metric Space
Author(s):
Samriddhi Ghosh, Ramakant Bhardwaj, Ritu Shrivastava, Vandana Rathore, Satyendra Narayan
Department of Mathematics,
Amity University, Kolkata, West Bengal,
India.
E-mail: ritha98@gmail.com
Department of Mathematics,
Amity University, Kolkata, West Bengal,
India.
E-mail: drrkbhardwaj100@gmail.com
Department of Mathematics,
Bahrain Polytechnic, Isa Town,
Kingdom of Bahrain
E-mail: ritu.shrivastava@polytechnic.bh
Faculty of Science and Technology,
Jagran Lakecity University, Bhopal, Madhya Pradesh,
India.
E-mail: drvandana@jlu.edu.in
School of Computer Science and
Technology,
Algoma University, Brampton, Ontario,
Canada.
E-mail: narayan.satyendra@gmail.com
Abstract:
The main aim of the research is to establish some invariant point (fixed point) results under the purview of R-Metric Spaces, for integral type R-contractive mappings. To serve this purpose, concepts of R-continuity, R-convergence and R-preservation has been used. Finally, the obtained results has been used to deduce some invariant point results for Banach, Kannan and Chatterjea type mappings in R-Metric Space. Also some examples and applications have been illustrated to support the findings discussed.
Paper's Title:
Results Concerning Fixed Point for Soft Weakly Contraction In Soft Metric Spaces
Author(s):
Abid Khan, Santosh Kumar Sharma, Anurag Choubey, Girraj Kumar Verma, Umashankar Sharma, Ramakant Bhardwaj
Department of Mathematics,
AUMP, Gwalior,
India.
abid69304@gmail.com
Department of Mathematics,
AUMP, Gwalior,
India.
sksharma1@gwa.amity.edu
Department of Computer Science,
Technocrats Institute of Technology,
Bhopal, MP,
India.
directoracademicstit@gmail.com
Department of Mathematics,
AUMP, Gwalior,
India.
gkverma@gwa.amity.edu
Department of Physics,
RJIT BSF Tekanpur, MP,
India.
ussharma001@gmail.com
School of Applied Science
AUK, WB,
India.
rkbhardwaj100@gmail.com
Abstract:
The basic objective of the proposed research work is to make people acquainted with the concept of soft metric space by generalizing the notions of soft (ψ,φ)-weakly contractive mappings in soft metric space, as well as to look at specific fundamental and topological parts of the underlying spaces. A compatible example is given to explain the idea of said space structure. The theory is very useful in decision making problems and secure transmission as fixed point provides exact output. The fixed-point theorems on subsets of Rm that are useful in game theoretic settings.
Paper's Title:
Random Fixed Point Result in Banach Space
Author(s):
1Anwesha Ghorai, 2Samriddhi Ghosh, 3Sneha Khandait, 4Aditya Ghosh, 5Ramakant Bhardwaj, 6Satyendra Narayan
1
Department of Mathematics,3Engineering
Science and Humanities department,
Thakur College of Engineering and Technology, Mumbai, Maharashtra,
India.
E-mail: sneha.khandait@tcetmumbai.in
4Department
of Mathematics,
Amity University, Kolkata, West Bengal,
India.
E-mail: ghosh.aditya.iitg08@gmail.com
5Department
of Mathematics,
Amity University, Kolkata, West Bengal,
India.
E-mail: drrkbhardwaj@gmail.com
6School
of Computer Science and Technology,
Algoma University, Brampton, Ontario,
Canada.
E-mail: narayan.satyendra@gmail.com
Abstract:
The present paper deals with an extension of classical fixed point theory using random variable for advancement because it has far-reaching applications in calculus, optimization, and stochastic processes. However, many nonlinear operators arise in applied mathematics which do not fulfill the strict contraction conditions of the classical Banach principle. This limitation has inspired the development of generalized non-contractive mappings. New generalized contractive-type conditions for random operators in a complete probability measure space as well as Banach space are established. The proposed conditions incorporate nonlinear, fractional, and minimum-type terms. Random fixed point theorem are proved for rational inequalities. These results not only generalize existing theorems, but also contribute to further development of functional analysis and its applications in mathematical modeling.
Paper's Title:
A Note on Evaluation of a New Class of Integrals Involving Generalized Hypergeometric Function
Author(s):
Madhav Prasad Poudel, Dongkyu Lim*, Narayan Prasad Pahari, Arjun K. Rathie
School of Engineering,
Pokhara University, Pokhara-30, Kaski,
Nepal.
E-mail: pdmadav@gmail.com
Department of Mathematics Education,
Andong National University, Andong 36729,
Republic of Korea.
E-mail: dklim@anu.ac.kr
Central Department of Mathematics,
Tribhuvan University, Kirtipur, Kathmandu,
Nepal.
E-mail: nppahari@gmail.com
Department of Mathematics,
Vedant College of Engineering & Technology (Rajasthan Technical University),
Village: Tulsi,
Jakhamund, Dist. Bundi, Rajasthan State,
India.
E-mail:
arjunkumarrathie@gmail.com
Abstract:
In the theory of hypergeometric and generalized hypergeometric series, classical summation theorems such as those of Gauss, Gauss second, Bailey and Kummer for the series
2F1; Watson, Dixon, Whipple and Saalshutz play a key role. Applications of the above mentioned summation theorems are well known for the series
3F2. In our present investigation, we aim to evaluate twenty five new class of integrals involving generalized hypergeometric function in the form of a single integral of the form:
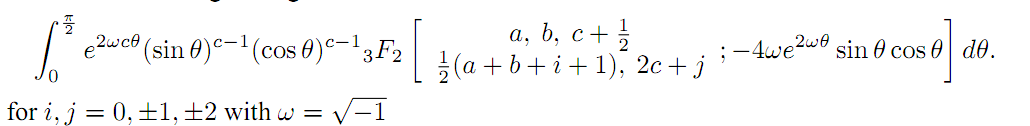
The results are established with the help of the generalizations of the classical Watson's summation theorem obtained earlier by Lavoie et al.. Fifty interesting integrals in the form of two integrals (twenty five each) have also been given as special cases of our main findings.
Paper's Title:
Using Direct and Fixed Point Technique of Cubic Functional Equation and its Hyers-Ulam Stability
Author(s):
Ramanuja Rao Kotti, Rajnesh Krishnan Mudaliar, Kaushal Neelam Devi, Shailendra Vikash Narayan
Fiji National University,
Department of Mathematics & Statistics,
P.O. Box 5529, Lautoka,
Fiji.
E-mail: ramanuja.kotti@fnu.ac.fj
URL: https://www.fnu.ac.fj
Abstract:
In this present work, we introduce a new type of finite dimensional cubic functional equation of the form
where Φ≥4 is an integer, and derive its general solution. The main purpose of this work is to investigate the Hyers-Ulam stability results for the above mentioned functional equation in Fuzzy Banach spaces by means of direct and fixed point methods.
Paper's Title:
Existence of Optimal Parameters for Damped Sine-Gordon Equation with Variable Diffusion Coefficient and Neumann Boundary Conditions
Author(s):
N. Thapa
Department of Mathematical Sciences,
Cameron University,
2800 West Gore Blvd,
73505 Lawton, Oklahoma,
USA.
E-mail: nthapa@cameron.edu
URL: http://www.cameron.edu/~nthapa/
Abstract:
The parameter identification problem for sine-Gordon equation is of a major interests among mathematicians and scientists.\ In this work we the consider sine-Gordon equation with variable diffusion coefficient and Neumann boundary data. We show the existence and uniqueness of weak solution for sine-Gordon equation. Then we show that the weak solution continuously depends on parameters. Finally we show the existence of optimal set of parameters.
Search and serve lasted 0 second(s).