|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Birkhoff-James orthogonality and Best Approximant in L1(X)
Author(s):
Mecheri Hacene and Rebiai Belgacem
Department of Mathematics and
Informatics,
LAMIS laboratory, University of Tebessa,
Algeria.
E-mail: mecherih2000@yahoo.fr
Department of Mathematics and
Informatics,
LAMIS laboratory, University of Tebessa,
Algeria.
E-mail: brebiai@gmail.com
Abstract:
Let X be a complex Banach space and let (X,ρ) be a positive measure space. The Birkhoff-James orthogonality is a generalization of Hilbert space orthogonality to Banach spaces. We use this notion of orthogonality to establish a new characterization of Birkhoff-James orthogonality of bounded linear operators in L1(X,ρ) also implies best approximation has been proved.
Paper's Title:
Weyl's theorem for class Q and k - quasi class Q Operators
Author(s):
S. Parvatham and D. Senthilkumar
Department of Mathematics and Humanities,
Sri Ramakrishna Institute of Technology, Coimbatore-10, Tamilnadu,
India.
E-mail: parvathasathish@gmail.com
Post Graduate and Research Department of
Mathematics,
Govt. Arts College, Coimbatore-641018, Tamilnadu,
India.
E-mail: senthilsenkumhari@gmail.com
Abstract:
In this paper, we give some properties of class Q operators. It is proved that every class Q operators satisfies Weyl's theorem under the condition that T2 is isometry. Also we proved that every k quasi class Q operators is Polaroid and the spectral mapping theorem holds for this class of operator. It will be proved that single valued extension property, Weyl and generalized Weyl's theorem holds for every k quasi class Q operators.
Paper's Title:
On the Class of Totally Polynomially Posinormal Operators
Author(s):
E. Shine Lal, T. Prasad, P. Ramya
Department of Mathematics,University
College,
Thiruvananthapuram, Kerala, 695034.
India.
E-mail: shinelal.e@gmail.com
Department of Mathematics,
University of Calicut,
Malapuram, Kerala 673635,
India.
E-mail: prasadvalapil@gmail.com
Department of Mathematics,
N.S.S College,
Nemmara, Kerala, 678508
India.
E-mail: ramyagcc@gmail.com
Abstract:
In this paper, we proved that if T ∈
B(H) is totally P-posinormal operator with
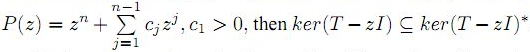 . Moreover, we study spectral continuity and range kernel orthogonality of these class of operators.
. Moreover, we study spectral continuity and range kernel orthogonality of these class of operators.
Search and serve lasted 1 second(s).