|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
Fixed Point Theorems for a Finite Family of Asymptotically Nonexpansive Mappings
Author(s):
E. Prempeh
Department of Mathematics,
Kwame Nkrumah University of Science and Technology,
Kumasi, Ghana
edward_prempeh2000@yahoo.com
Abstract:
Let
![]() be a real reflexive Banach space with a uniformly Gâteaux differentiable norm,
be a real reflexive Banach space with a uniformly Gâteaux differentiable norm,
![]() be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of
![]() i=1,2,...,r be a finite family of asymptotically nonexpansive mappings
such that for each
i=1,2,...,r be a finite family of asymptotically nonexpansive mappings
such that for each
![]()
![]() Let
Let
![]() be a nonempty set of common fixed points of
be a nonempty set of common fixed points of
![]() and define
and define
![]()
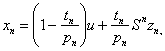
![]() associated with
associated with
![]() , converges strongly to a fixed point of
, converges strongly to a fixed point of
![]() provided
provided
![]() possesses uniform normal structure. Furthermore we prove that the iterative process:
possesses uniform normal structure. Furthermore we prove that the iterative process:
![]()
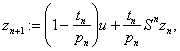
![]() , converges strongly to a fixed point of
, converges strongly to a fixed point of
![]()
Paper's Title:
On the Regularization of Hammerstein's type Operator Equations
Author(s):
E. Prempeh, I. Owusu-Mensah and K. Piesie-Frimpong
Department of Mathematics,
KNUST, Kumasi-
Ghana.
Department of Science Education,
University of Education,
Winneba
Department of Mathematics,
Presbyterian University College, Abetifi,
Ghana
E-mail: isaacowusumensah@gmail.com
E-mail: eprempeh.cos@knust.edu.gh
E-mail: piesie74@yahoo.com
Abstract:
We have studied Regularization of Hammerstein's Type Operator Equations in general Banach Spaces. In this paper, the results have been employed to establish regularized solutions to Hammerstein's type operator equations in Hilbert spaces by looking at three cases of regularization.
Search and serve lasted 1 second(s).