Paper's Title:

Fekete-Szegö Inequality for Sakaguchi Type of functions in Petal Shaped Domain

Author(s):

E. K. Nithiyanandham and B. Srutha Keerthi

Division of Mathematics, School of Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: nithiyankrish@gmail.com

Division of Mathematics, School of Advanced Sciences,
Vellore Institute of Technology Chennai Campus,
Chennai - 600 048,
India.
E-mail: keerthivitmaths@gmail.com

Abstract:

In this paper, we estimate coefficient bounds,|a_2|,|a_3| and |a_4|, Fekete-Szegö inequality and Toeplitz determinant T₂(2) and T₃(1) for functions belonging to the following class

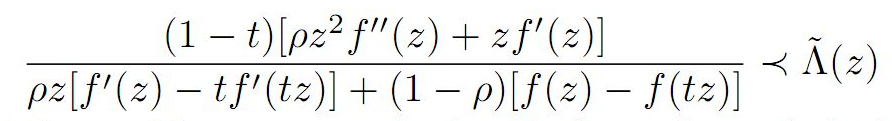
the function being holomorphic, we expand using Taylor series and obtain several corollaries and consequences for the main result.

Paper's Title:

Some Double λ-Convergent Sequence Spaces Over n-Normed Spaces

Author(s):

Kuldip Raj, Renu Anand and Seema Jamwal

School of Mathematics,
Shri Mata Vaishno Devi University Katra-182320,
Jammu and Kashmir,
India.

E-mail: kuldipraj68@gmail.com,  renuanand71@gmail.com, seemajamwal8@gmail.com

Abstract:

In this paper we introduce some double generalized λ-convergent sequence spaces over n-normed spaces defined by Musielak-Orlicz function M = (M_k,l). We also made an attempt to study some topological and algebraic properties of these sequence spaces.

Paper's Title:

Inequalities for Discrete F-Divergence Measures: A Survey of Recent Results

Author(s):

Sever S. Dragomir^1,2

¹Mathematics, School of Engineering & Science
Victoria University, PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au

 
²DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL: http://rgmia.org/dragomir 

Abstract:

In this paper we survey some recent results obtained by the author in providing various bounds for the celebrated f-divergence measure for various classes of functions f. Several techniques including inequalities of Jensen and Slater types for convex functions are employed. Bounds in terms of Kullback-Leibler Distance, Hellinger Discrimination and Varation distance are provided. Approximations of the f-divergence measure by the use of the celebrated Ostrowski and Trapezoid inequalities are obtained. More accurate approximation formulae that make use of Taylor's expansion with integral remainder are also surveyed. A comprehensive list of recent papers by several authors related this important concept in information theory is also included as an appendix to the main text.

Paper's Title:

Szegö Limits and Haar Wavelet Basis

Author(s):

M. N. N. Namboodiri and S. Remadevi

Dept. of Mathematics, Cochin University of Science and Technology,
Cochin-21, Kerala,
India.

nambu@cusat.ac.in

Dept. of Mathematics, College of Engineering,
Cherthala, Kerala,
India.

rema@mec.ac.in
 

Abstract:

This paper deals with Szegö type limits for multiplication operators on L² (R) with respect to Haar orthonormal basis. Similar studies have been carried out by Morrison for multiplication operators T_f using Walsh System and Legendre polynomials [14]. Unlike the Walsh and Fourier basis functions, the Haar basis functions are local in nature. It is observed that Szegö type limit exist for a class of multiplication operators T_f , f∈ L^∞ (R) with respect to Haar (wavelet) system with appropriate ordering. More general classes of orderings of Haar system are identified for which the Szegö type limit exist for certain classes of multiplication operators. Some illustrative examples are also provided.

Search and serve lasted 1 second(s).