|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
On Finding Integrating Factors and First Integrals for a Class of Higher Order Differential Equations
Author(s):
Mohammadkheer M. Al-Jararha
Department of Mathematics,
Yarmouk University,
Irbid, 21163,
Jordan.
E-mail: mohammad.ja@yu.edu.jo
Abstract:
If the $n-th$ order differential equation is not exact, under certain
conditions, an integrating factor exists which transforms the differential
equation into an exact one. Thus, the order of differential equation can be
reduced to the lower order. In this paper, we present a technique for finding
integrating factors of the following class of differential equations:
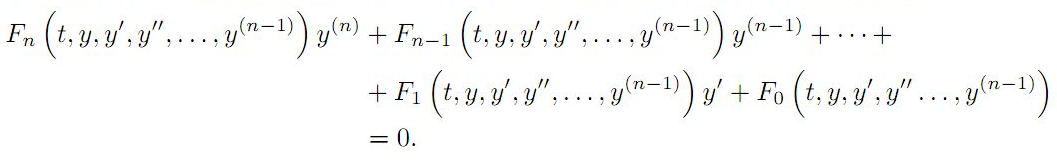
Here, the functions F0,F1,F2,
…,Fn are assumed to be continuous
functions with their first partial derivatives on some simply connected domain
Ω ⊂ Rn+1.
We also presented some demonstrative examples
Paper's Title:
Integrating Factors and First Integrals of a Class of Third Order Differential Equations
Author(s):
Mohammadkheer Al-Jararha
Department of Mathematics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: mohammad.ja@yu.edu.jo
Abstract:
The principle of finding an integrating factor for a none exact differential equations is extended to a class of third order differential equations. If the third order equation is not exact, under certain conditions, an integrating factor exists which transforms it to an exact one. Hence, it can be reduced into a second order differential equation. In this paper, we give explicit forms for certain integrating factors of a class of the third order differential equations.
Paper's Title:
Inequalities of Gamma Function Appearing in Generalizing Probability Sampling Design
Author(s):
Mohammadkheer M. Al-Jararha And Jehad M. Al-Jararha
Department of Mathematics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: mohammad.ja@yu.edu.jo
Department of Statistics,
Yarmouk University,
Irbid 21163,
Jordan.
E-mail: jehad@yu.edu.jo
Abstract:
In this paper, we investigate the complete monotonicity of some functions involving gamma function. Using the monotonic properties of these functions, we derived some inequalities involving gamma and beta functions. Such inequalities can be used to generalize different probability distribution functions. Also, they can be used to generalize some statistical designs, e.g., the probability proportional to the size without replacement design.
Search and serve lasted 0 second(s).