|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper Title:
Fixed Point Theorems for a Finite Family of Asymptotically Nonexpansive Mappings
Author(s):
E. Prempeh
Department of Mathematics,
Kwame Nkrumah University of Science and Technology,
Kumasi, Ghana
edward_prempeh2000@yahoo.com
Abstract:
Let
be a real reflexive Banach space with a uniformly Gâteaux differentiable norm,
be a nonempty bounded closed convex subset of
i=1,2,...,r be a finite family of asymptotically nonexpansive mappings
such that for each
Let
be a nonempty set of common fixed points of
and define
. Let
be fixed and let
be such that
as
. We can prove that the sequence
satisfying the relation
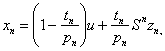
associated with
, converges strongly to a fixed point of
provided
possesses uniform normal structure. Furthermore we prove that the iterative process:
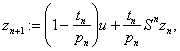
, converges strongly to a fixed point of
Full Text PDF:
