|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper's Title:
A Generalization of a Trace Inequality for Positive Definite Matrices
Author(s):
E. V. Belmega, M. Jungers, and S. Lasaulce
Université Paris-Sud Xi, SUPELEC,
Laboratoire Des Signaux Et Systèmes,
Gif-Sur-Yvette,
France.
belmega@lss.supelec.fr
http://veronica.belmega.lss.supelec.fr
CNRS, ENSEM, CRAN, Vandoeuvre,
France.
marc.jungers@cran.uhp-nancy.fr
http://perso.ensem.inpl-nancy.fr/Marc.Jungers/
CNRS, SUPELEC, Laboratoire des Signaux et
Systèmes,
Gif-Sur-Yvette,
France.
lasaulce@lss.supelec.fr
http://samson.lasaulce.lss.supelec.fr
Abstract:
In this note, we provide a generalization of the trace inequality derived in [Belmega].
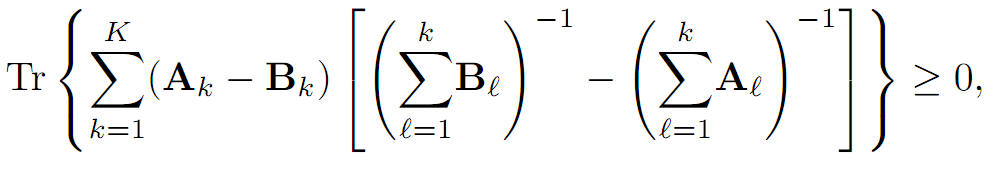
More precisely, we prove that for arbitrary K ≥ 1 where Tr(∙) denotes the matrix trace operator, A1, B1 are any positive definite matrices and Ak, Bk for all k∈{2,...,k}, are any positive semidefinite matrices.
Paper's Title:
Refinements of the Trace Inequality of Belmega, Lasaulce and Debbah
Author(s):
Shigeru Furuichi and Minghua Lin
Department of Computer Science and System Analysis,
College of Humanities and Sciences, Nihon University,
3-25-40, Sakurajyousui, Setagaya-ku, Tokyo, 156-8550, Japan.
Department of Mathematics and
Statistics,
University of Regina, Regina, Saskatchewan, Canada S4S 0A2.
furuichi@chs.nihon-u.ac.jp, lin243@uregina.ca.
Abstract:
In this short paper, we show a certain matrix trace inequality and then give a refinement of the trace inequality proven by Belmega, Lasaulce and Debbah. In addition, we give an another improvement of their trace inequality.
Paper's Title:
Trace Inequalities for Operators in Hilbert Spaces: a Survey of Recent Results
Author(s):
Sever S. Dragomir1,2
1Mathematics,
School of Engineering
& Science
Victoria University,
PO Box 14428
Melbourne City, MC 8001,
Australia
E-mail: sever.dragomir@vu.edu.au
2DST-NRF Centre of Excellence in the Mathematical and Statistical Sciences,
School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa
URL:
https://rgmia.org/dragomir
Abstract:
In this paper we survey some recent trace inequalities for operators in Hilbert spaces that are connected to Schwarz's, Buzano's and Kato's inequalities and the reverses of Schwarz inequality known in the literature as Cassels' inequality and Shisha-Mond's inequality. Applications for some functionals that are naturally associated to some of these inequalities and for functions of operators defined by power series are given. Further, various trace inequalities for convex functions are presented including refinements of Jensen inequality and several reverses of Jensen's inequality. Hermite-Hadamard type inequalities and the trace version of Slater's inequality are given. Some Lipschitz type inequalities are also surveyed. Examples for fundamental functions such as the power, logarithmic, resolvent and exponential functions are provided as well.
Search and serve lasted 0 second(s).