|
|
The Australian Journal of Mathematical Analysis and Applications
ISSN 1449-5910 |
|
||||||||||||
|
|
||||||||||||
Paper Title:
Some interesting properties of finite continuous CesÓro operators
Author(s):
Abdelouahab Mansour and Abderrazak Hechifa
Operator theory laboratory (LABTHOP),
Eloued University,
Algeria.
E-mail:
amansour@math.univ-lyon1.fr
Mathematics Department,
Faculty of Science,
Badji Mokhtar University, -Annaba,
Algeria.
E-mail:
abderrazak02@gmail.com
Abstract:
A complex scalar λ is called an extended eigenvalue of a bounded linear operator T on a complex Banach space if there is a nonzero operator X such that TX = λ XT, the operator X is called extended eigenoperator of T corresponding to the extended eigenvalue λ.
In this paper we prove some properties of extended eigenvalue and extended eigenoperator for
C1 on Lp([0,1]), where C1 is the CesÓro operator defined on the complex Banach spaces Lp([0 , 1]) for
1<p<∞ by the expression
Full Text PDF: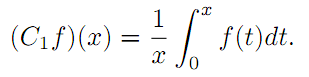
ę 2004-2023 Austral Internet Publishing