Paper Title:

Some New Inequalities for Hypo-q-Norms on a Cartesian Product of Normed Linear Spaces

Author(s):

Sever S. Dragomir^1,2

¹Applied Mathematics Research Group, ISILC,
Victoria University,
PO Box 14428, Melbourne City, MC 8001,
Australia.
E-mail: sever.dragomir@vu.edu.au
URL: http://rgmia.org/dragomir 

 
²School of Computer Science & Applied Mathematics,
University of the Witwatersrand,
Private Bag 3, Johannesburg 2050,
South Africa.
 

Abstract:

Let ( E,|| · ||)  be a normed linear space over the real or complex number field K. If by S_n,p  with p∈[ 1,∞]  we denote the spheres generated by the $p$-norms || · ||_n,p  on Kⁿ, then we consider the following hypo-q-norms on 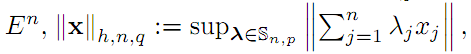 with q>1 and 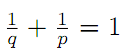if p>1, q=1 if p=∞ and q=∞ if p=1. For p=2, we also consider the hypo-Euclidean norm on Eⁿ, i.e.,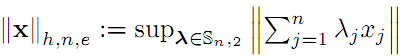

In this paper we have obtained among others the following inequalities

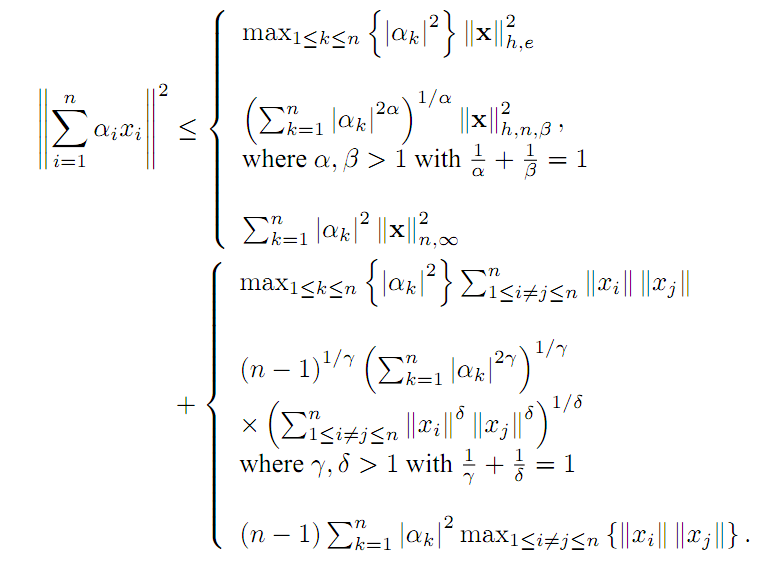
The case for n=2 and the connection with the following new norms and

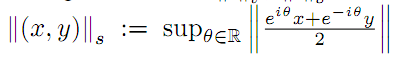
 are also investigated. When the norm || · || is generated by an inner product, further bounds are given as well.

Full Text PDF: