Paper Title:

A Note on Evaluation of a New Class of Integrals Involving Generalized Hypergeometric Function

Author(s):

Madhav Prasad Poudel, Dongkyu Lim^*, Narayan Prasad Pahari, Arjun K. Rathie

School of Engineering,
Pokhara University, Pokhara-30, Kaski,
Nepal.
E-mail: pdmadav@gmail.com

Department of Mathematics Education,
Andong National University, Andong 36729,
Republic of Korea.
E-mail: dklim@anu.ac.kr

Central Department of Mathematics,
Tribhuvan University, Kirtipur, Kathmandu,
Nepal.
E-mail: nppahari@gmail.com

Department of Mathematics,
Vedant College of Engineering & Technology (Rajasthan Technical University), Village: Tulsi,
Jakhamund, Dist. Bundi, Rajasthan State,
India.
E-mail: arjunkumarrathie@gmail.com

Abstract:

In the theory of hypergeometric and generalized hypergeometric series, classical summation theorems such as those of Gauss, Gauss second, Bailey and Kummer for the series ₂F₁; Watson, Dixon, Whipple and Saalshutz play a key role. Applications of the above mentioned summation theorems are well known for the series ₃F₂. In our present investigation, we aim to evaluate twenty five new class of integrals involving generalized hypergeometric function in the form of a single integral of the form:

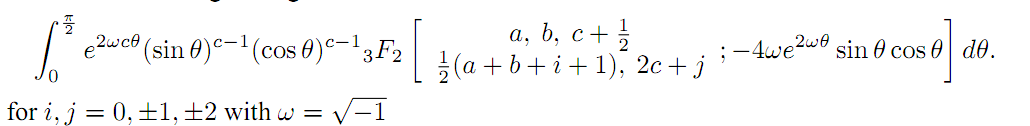
The results are established with the help of the generalizations of the classical Watson's summation theorem obtained earlier by Lavoie et al.. Fifty interesting integrals in the form of two integrals (twenty five each) have also been given as special cases of our main findings.

Full Text PDF: